Home | Develop | Download | Contact
defines | Funciones | Variables
funciónes del módulo PdsMath.

defines

#define PDS_PHI   1.618033988749894
 Es equivalente a (1+sqrt(5))/2. El llamado número aureo. Más...
 
#define PDS_GOLDEN_RATIO   PDS_PHI
 Es equivalente a PDS_PHI = (1+sqrt(5))/2. El llamado número aureo. Más...
 
#define PDS_1_OVER_SQRT_2PI   0.398942280401433
 Es equivalente a 1/sqrt(2*M_PI). Más...
 
#define PDS_2_OVER_SQRT_PI   1.12837916709551
 Es equivalente a 2/sqrt(M_PI). Más...
 
#define PDS_LN2   6.93147180559945e-01
 Es equivalente a ln(2). Más...
 

Funciones

double pds_qfunc (double x)
 Evalúa la función Q(x) Más...
 
double pds_qfuncinv (double q)
 Evalúa la función Q^{-1}(q) , función Q inversa. Más...
 
double pds_gamma (double x)
 Evalúa la función gamma(x) Más...
 
double pds_erf (double x)
 Evalúa la función erf(x) Más...
 
double pds_erfc (double x)
 Evalúa la función erfc(x) Más...
 
double pds_sgn (double x)
 Evalúa la función signo sgn(x) Más...
 
int pds_isgn (int x)
 Evalúa la función signo sgn(x) Más...
 
double pds_sinc (double x)
 Evalúa la función sinc(x)=sin(x)/x. Más...
 
double pds_sigmoid (double x)
 Evalúa la función sigmoid(x)=1/(1+e^{-x}) Más...
 
double pds_gauss (double x, double U, double Sigma)
 Evalúa la función gaussiana, o distribución gaussiana f(x)=N(U,Sigma^2). Más...
 
double pds_gauss2 (double x, double U, double Sigma2)
 Evalúa la función gaussiana, o distribución gaussiana f(x)=N(U,Sigma2). Más...
 
double pds_gnorm (double x)
 Evalúa la función gaussiana normalizada, o distribución gaussiana f(x)=N(0,1.0). Más...
 
double pds_exp22 (double x)
 Evalúa la función f(x)=exp(-x^2/2). Más...
 
double pds_exp2 (double x)
 Evalúa la función f(x)=exp(-x^2). Más...
 
double pds_exp1 (double x)
 Evalúa la función f(x)=exp(-x). Más...
 
double pds_r1exp1 (double x, double r)
 Evalúa la función f(x)=pow(x,r-1.0)*exp(-x). Más...
 
double pds_hb (double x)
 Evalúa la función de entropía binaria Hb(x)=-x*log2(x)-(1-x)*log2(1-x). Más...
 
double pds_hbinv (double h)
 Retorna el valor x de la función de entropía binaria para un valor de h aproximadamente igual a Hb(x)=-x*log2(x)-(1-x)*log2(1-x). Más...
 
double pds_nchoosek (unsigned int n, unsigned int k)
 Retorna el combinatorio (n,k) Más...
 
double pds_binomial (unsigned int n, unsigned int k, double p)
 Retorna la distribucion binomial(n,k,p) Más...
 
double pds_integration (double(*f)(double), double a, double b, unsigned int n)
 Evalúa la integral de a–>b de la función f(x), aplicando la regla de Simpson con n divisiones, si n no es par internamente la función hace n=n+1. Más...
 
double pds_integration1p (double(*f)(double, double), double r, double a, double b, unsigned int n)
 Evalúa la integral de a–>b de la función f(x,r), aplicando la regla de Simpson con n divisiones, si n no es par internamente la función hace n=n+1. Más...
 
double pds_integration_with_eval_funcs (double(*f)(double), double a, double b, double fa, double fb, unsigned int n)
 Evalúa la integral de a–>b de la función f(x), aplicando la regla de Simpson con n divisiones, si n no es par internamente la función hace n=n+1. f(a) e f(b) n sn evaluados pues ests datos son entregados como variables de entrada. Más...
 
double pds_integration_inf (double(*f)(double), double a, unsigned int n)
 Evalúa la integral de a–>infinito de la función f(x), aplicando el cambio de variable u<–1/(x+1) para integrar de 0–>1/(a+1) y ejecutar luego la regla de Simpson con n divisiones, si n no es par internamente la función hace n=n+1. Además es necesario que el limite de f(1/u-1)/u^2–>0 cuando u–>0. Más...
 
double pds_integration1p_inf (double(*f)(double, double), double r, double a, unsigned int n)
 Evalúa la integral de a–>infinito de la función f(x,r) en x, aplicando el cambio de variable u<–1/(x+1) para integrar de 0–>1/(a+1) y ejecutar luego la regla de Simpson con n divisiones, si n no es par internamente la función hace n=n+1. Además es necesario que el limite de f(1/u-1,r)/u^2–>0 cuando u–>0. Más...
 

Variables

static const unsigned long int PDS_MPB10 [] ={0,7,97,997,9973,99991,999983,9999991}
 Es un arreglo de variables enteras con números primos de modo que PDS_MPB10[d] contiene el máximo número primo en base 10 con "d" decimales. El máximo valor de "d" es PDS_LENGTH_MPB10-1;. Más...
 
static const unsigned long int PDS_LENGTH_MPB10 =8
 Es el número de elementos del arreglo PDS_MPB10 . Más...
 

Descripción detallada

Documentación de los 'defines'

◆ PDS_PHI

#define PDS_PHI   1.618033988749894

Es equivalente a (1+sqrt(5))/2. El llamado número aureo.

\[ PDS\_PHI=\frac{1+\sqrt{5}}{2}\]

Definición en la línea 46 del archivo pdsmath.h.

◆ PDS_GOLDEN_RATIO

#define PDS_GOLDEN_RATIO   PDS_PHI

Es equivalente a PDS_PHI = (1+sqrt(5))/2. El llamado número aureo.

\[ PDS\_GOLDEN\_RATIO=\frac{1+\sqrt{5}}{2}\]

Definición en la línea 55 del archivo pdsmath.h.

◆ PDS_1_OVER_SQRT_2PI

#define PDS_1_OVER_SQRT_2PI   0.398942280401433

Es equivalente a 1/sqrt(2*M_PI).

\[ PDS\_1\_OVER\_SQRT\_2PI=\frac{1}{\sqrt{2 \pi}}\]

Definición en la línea 63 del archivo pdsmath.h.

◆ PDS_2_OVER_SQRT_PI

#define PDS_2_OVER_SQRT_PI   1.12837916709551

Es equivalente a 2/sqrt(M_PI).

\[ PDS\_2\_OVER\_SQRT\_PI=\frac{2}{\sqrt{\pi}}\]

Definición en la línea 71 del archivo pdsmath.h.

◆ PDS_LN2

#define PDS_LN2   6.93147180559945e-01

Es equivalente a ln(2).

\[ PDS\_LN2=ln(2)\]

Definición en la línea 79 del archivo pdsmath.h.

Documentación de las funciones

◆ pds_qfunc()

double pds_qfunc ( double  x)

Evalúa la función Q(x)

\[ y=Q(x)=\frac{1}{\sqrt{2\pi}}\int_{x}^{\infty}exp({-\frac{u^2}{2}})du \]

Parámetros
[in]xValor de entrada.
Devuelve
El valor de Q(x).
Ejemplos:
example_qfunc.c.

◆ pds_qfuncinv()

double pds_qfuncinv ( double  q)

Evalúa la función Q^{-1}(q) , función Q inversa.

\[ x=Q^{-1}(q) \]

\[ q=Q(x)=\frac{1}{\sqrt{2\pi}}\int_{x}^{\infty}exp({-\frac{u^2}{2}})du \]

Parámetros
[in]qValor de entrada.
Devuelve
El valor x.
Ejemplos:
example_qfunc.c.

◆ pds_gamma()

double pds_gamma ( double  x)

Evalúa la función gamma(x)

\[ \Gamma(x)=\int _{0}^{\infty }t^{x-1}e^{-t}\,dt \]

Parámetros
[in]xValor de entrada.
Devuelve
El valor de gamma(x).
Ejemplos:
example_gamma.c.

◆ pds_erf()

double pds_erf ( double  x)

Evalúa la función erf(x)

\[ y=erf(x)=\frac{2}{\sqrt{\pi}}\int_{0}^{x}exp({-u^2})du \]

Parámetros
[in]xValor de entrada.
Devuelve
El valor de erf(x).

◆ pds_erfc()

double pds_erfc ( double  x)

Evalúa la función erfc(x)

\[ y=erfc(x)=1-\frac{2}{\sqrt{\pi}}\int_{0}^{x}exp({-u^2})du \]

Parámetros
[in]xValor de entrada.
Devuelve
El valor de erfc(x).

◆ pds_sgn()

double pds_sgn ( double  x)

Evalúa la función signo sgn(x)

\[y=sgn(x)=\]

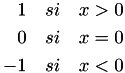
\begin{eqnarray*} 1 &si& x>0 \\ 0 &si& x=0 \\ -1 &si& x<0 \end{eqnarray*}

Parámetros
[in]xValor de entrada.
Devuelve
El valor de sgn(x).

◆ pds_isgn()

int pds_isgn ( int  x)

Evalúa la función signo sgn(x)

\[y=sgn(x)=\]

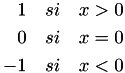
\begin{eqnarray*} 1 &si& x>0 \\ 0 &si& x=0 \\ -1 &si& x<0 \end{eqnarray*}

Parámetros
[in]xValor de entrada.
Devuelve
El valor de sgn(x).

◆ pds_sinc()

double pds_sinc ( double  x)

Evalúa la función sinc(x)=sin(x)/x.

\[y=sinc(x)=\frac{sin(x)}{x}\]

Parámetros
[in]xValor de entrada.
Devuelve
El valor de sinc(x).

◆ pds_sigmoid()

double pds_sigmoid ( double  x)

Evalúa la función sigmoid(x)=1/(1+e^{-x})

\[y=sigmoid(x)=\frac{1}{1+e^{-x}}\]

Parámetros
[in]xValor de entrada.
Devuelve
El valor de sigmoid(x).

◆ pds_gauss()

double pds_gauss ( double  x,
double  U,
double  Sigma 
)

Evalúa la función gaussiana, o distribución gaussiana f(x)=N(U,Sigma^2).

\[y=\frac{1}{\sqrt{2\pi \sigma^2}}e^{-\frac{(x-U)^2}{2\sigma^2}}\]

Parámetros
[in]xValor de entrada.
[in]UEl valor medio de x.
[in]SigmaEs desvío padrón de x.
Devuelve
El valor de f(x)=N(U,Sigma^2).

◆ pds_gauss2()

double pds_gauss2 ( double  x,
double  U,
double  Sigma2 
)

Evalúa la función gaussiana, o distribución gaussiana f(x)=N(U,Sigma2).

\[y=\frac{1}{\sqrt{2\pi \sigma^2}}e^{-\frac{(x-U)^2}{2\sigma^2}}\]

Parámetros
[in]xValor de entrada.
[in]UEl valor medio de x.
[in]Sigma2Es la varianza de x, Sigma^2.
Devuelve
El valor de f(x)=N(U,Sigma^2).

◆ pds_gnorm()

double pds_gnorm ( double  x)

Evalúa la función gaussiana normalizada, o distribución gaussiana f(x)=N(0,1.0).

\[y=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}\]

Parámetros
[in]xValor de entrada.
Devuelve
El valor de f(x)=N(0,1.0).

◆ pds_exp22()

double pds_exp22 ( double  x)

Evalúa la función f(x)=exp(-x^2/2).

\[y=e^{-\frac{x^2}{2}}\]

Parámetros
[in]xValor de entrada.
Devuelve
El valor de f(x).

◆ pds_exp2()

double pds_exp2 ( double  x)

Evalúa la función f(x)=exp(-x^2).

\[y=e^{-x^2}\]

Parámetros
[in]xValor de entrada.
Devuelve
El valor de f(x).

◆ pds_exp1()

double pds_exp1 ( double  x)

Evalúa la función f(x)=exp(-x).

\[y=e^{-x}\]

Parámetros
[in]xValor de entrada.
Devuelve
El valor de f(x).

◆ pds_r1exp1()

double pds_r1exp1 ( double  x,
double  r 
)

Evalúa la función f(x)=pow(x,r-1.0)*exp(-x).

\[y=x^{r-1}e^{-x}\]

Parámetros
[in]xValor de entrada.
[in]rValor del parámetro.
Devuelve
El valor de f(x,r).

◆ pds_hb()

double pds_hb ( double  x)

Evalúa la función de entropía binaria Hb(x)=-x*log2(x)-(1-x)*log2(1-x).

\[H_b(x)\equiv -x log_2(x)-(1-x) log_2(1-x)\]

Parámetros
[in]xValor de entrada.
Devuelve
El valor de Hb(x).
Ejemplos:
example_hb.c.

◆ pds_hbinv()

double pds_hbinv ( double  h)

Retorna el valor x de la función de entropía binaria para un valor de h aproximadamente igual a Hb(x)=-x*log2(x)-(1-x)*log2(1-x).

\[h=H_b(x)\equiv -x log_2(x)-(1-x) log_2(1-x)\]

Parámetros
[in]hValor de entrada.
Devuelve
El valor de x en h=Hb(x). La busqueeda finaliza quando |h-Hb(p)|<|E(h)/1000000|, E(h)=h +(1-2 h) u(h-0.5).
Ejemplos:
example_hb.c.

◆ pds_nchoosek()

double pds_nchoosek ( unsigned int  n,
unsigned int  k 
)

Retorna el combinatorio (n,k)

\[ {n \choose k}=\frac{n!}{k!(n-k)!} \]

Parámetros
[in]nValor superior del combinatorio.
[in]kValor inferior del combinatorio.
Devuelve
El valor del combinatorio (n,k).

◆ pds_binomial()

double pds_binomial ( unsigned int  n,
unsigned int  k,
double  p 
)

Retorna la distribucion binomial(n,k,p)

\[ f(n,k,p)={n \choose k} p^k (1-p)^{n-k}\]

Parámetros
[in]nNumero total de ensayos
[in]kNumero de eventos encontrdos.
[in]pprobbilidad de contecer un evento en un ensayo.
Devuelve
El valor de f(n,k,p).

◆ pds_integration()

double pds_integration ( double(*)(double)  f,
double  a,
double  b,
unsigned int  n 
)

Evalúa la integral de a–>b de la función f(x), aplicando la regla de Simpson con n divisiones, si n no es par internamente la función hace n=n+1.

\[S_n=\int_{a}^{b}f(x)dx\]

\[h=\frac{b-a}{n}\]

\[x_i=a+h~i\]

\[S_n=\frac{h}{3}(f(x_0)+f(x_n)+4\left [ f(x_1)+f(x_3)+\cdots +f(x_{n-1}) \right ]+2\left [ f(x_2)+f(x_4)+\cdots +f(x_{n-2}) \right ])\]

Parámetros
[in]fLa función a integrar.
[in]aLímite inferior de la integral.
[in]bLímite superior de la integral.
[in]nEs el número de divisiones.
Devuelve
El valor de la integral o cero si hubo un error, ejemplo b<a o n<=0.

◆ pds_integration1p()

double pds_integration1p ( double(*)(double, double)  f,
double  r,
double  a,
double  b,
unsigned int  n 
)

Evalúa la integral de a–>b de la función f(x,r), aplicando la regla de Simpson con n divisiones, si n no es par internamente la función hace n=n+1.

\[S_n=\int_{a}^{b}f(x,r)dx\]

\[h=\frac{b-a}{n}\]

\[x_i=a+h~i\]

\[S_n=\frac{h}{3}(f(x_0,r)+f(x_n,r)+4\left [ f(x_1,r)+f(x_3,r)+\cdots +f(x_{n-1},r) \right ]+2\left [ f(x_2,r)+f(x_4,r)+\cdots +f(x_{n-2},r) \right ])\]

Parámetros
[in]fLa función a integrar.
[in]rVariable libre.
[in]aLímite inferior de la integral.
[in]bLímite superior de la integral.
[in]nEs el número de divisiones.
Devuelve
El valor de la integral o cero si hubo un error, ejemplo b<a o n<=0.

◆ pds_integration_with_eval_funcs()

double pds_integration_with_eval_funcs ( double(*)(double)  f,
double  a,
double  b,
double  fa,
double  fb,
unsigned int  n 
)

Evalúa la integral de a–>b de la función f(x), aplicando la regla de Simpson con n divisiones, si n no es par internamente la función hace n=n+1. f(a) e f(b) n sn evaluados pues ests datos son entregados como variables de entrada.

\[S_n=\int_{a}^{b}f(x)dx\]

\[h=\frac{b-a}{n}\]

\[x_i=a+h~i\]

\[S_n=\frac{h}{3}(f(a)+f(b)+4\left [ f(x_1)+f(x_3)+\cdots +f(x_{n-1}) \right ]+2\left [ f(x_2)+f(x_4)+\cdots +f(x_{n-2}) \right ])\]

Parámetros
[in]fLa función a integrar.
[in]aLímite inferior de la integral.
[in]bLímite superior de la integral.
[in]faEl resultado de evaluar f(a).
[in]fbEl resultado de evaluar f(b).
[in]nEs el número de divisiones.
Devuelve
El valor de la integral o cero si hubo un error, ejemplo b<a o n<=0.

◆ pds_integration_inf()

double pds_integration_inf ( double(*)(double)  f,
double  a,
unsigned int  n 
)

Evalúa la integral de a–>infinito de la función f(x), aplicando el cambio de variable u<–1/(x+1) para integrar de 0–>1/(a+1) y ejecutar luego la regla de Simpson con n divisiones, si n no es par internamente la función hace n=n+1. Además es necesario que el limite de f(1/u-1)/u^2–>0 cuando u–>0.

\[ if( a \geq 0) \quad S_t= \int_{x_{0}=a}^{ \infty }f(x)dx \]

\[ if( a < 0) \quad S_t= \int_{a}^{0}f(x)dx + \int_{x_{0}=0}^{ \infty }f(x)dx \]

\[ \left.\int_{x_{0}}^{ \infty }f(x)dx\right|_{u=\frac{1}{x+1}} \rightarrow \int_{0}^{ \frac{1}{x_{0}+1} }\frac{f(\frac{1}{u}-1)}{u^2}du \]

Se asume que

\[ \lim_{u \rightarrow 0+}\frac{f(\frac{1}{u}-1)}{u^2}=0 \]

Parámetros
[in]fLa función a integrar.
[in]aLímite inferior de la integral.
[in]nEs el número de divisiones.
Devuelve
El valor de la integral o cero si hubo un error, ejemplo b<a o n<=0.

◆ pds_integration1p_inf()

double pds_integration1p_inf ( double(*)(double, double)  f,
double  r,
double  a,
unsigned int  n 
)

Evalúa la integral de a–>infinito de la función f(x,r) en x, aplicando el cambio de variable u<–1/(x+1) para integrar de 0–>1/(a+1) y ejecutar luego la regla de Simpson con n divisiones, si n no es par internamente la función hace n=n+1. Además es necesario que el limite de f(1/u-1,r)/u^2–>0 cuando u–>0.

\[ if(a \geq 0) \quad S_t= \int_{x_{0}=a}^{ \infty }f(x,r)dx \]

\[ if(a < 0) \quad S_t= \int_{a}^{0}f(x,r)dx + \int_{x_{0}=0}^{ \infty }f(x,r)dx \]

\[ \left. \int_{x_{0}}^{ \infty }f(x,r)dx\right|_{u=\frac{1}{x+1}} \rightarrow \int_{0}^{ \frac{1}{x_{0}+1} }\frac{f(\frac{1}{u}-1,r)}{u^2}du \]

Se asume que

\[ \lim_{u \rightarrow 0+}\frac{f(\frac{1}{u}-1,r)}{u^2}=0 \]

Parámetros
[in]fLa función a integrar.
[in]rValor del parámetro .
[in]aLímite inferior de la integral.
[in]nEs el número de divisiones.
Devuelve
El valor de la integral o cero si hubo un error, ejemplo b<a o n<=0.

Documentación de las variables

◆ PDS_MPB10

PDS_MPB10 ={0,7,97,997,9973,99991,999983,9999991}
static

Es un arreglo de variables enteras con números primos de modo que PDS_MPB10[d] contiene el máximo número primo en base 10 con "d" decimales. El máximo valor de "d" es PDS_LENGTH_MPB10-1;.

Definición en la línea 88 del archivo pdsmath.h.

◆ PDS_LENGTH_MPB10

PDS_LENGTH_MPB10 =8
static

Es el número de elementos del arreglo PDS_MPB10 .

Definición en la línea 95 del archivo pdsmath.h.

Enlaces de interés

HomePage Bazaar Download Bug report Ayuda Developer Feed
Manual de referencia generado el Sábado, 23 de Mayo de 2020 20:42:03 para la biblioteca libpdsm usando  Generado el Sábado, 23 de Mayo de 2020 20:42:03 para libpdsm por   doxygen 1.8.13